| Мова : |
|
| Енциклопедія співтовариство |Енциклопедія відповіді |Відправити запитання |Словник знань |Завантажити знання |
Лінійного перетворення |
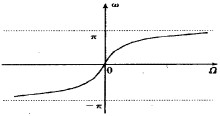      |
|
лінійне перетворення Визначення лінійного перетворення Лінійне простір V в себе, часто званий V відображення перетворення. Лінійне перетворення посиланням на фіг.Також має наступне визначення: Лінійне простір V називається перетворенням лінійної трансформації, якщо будь-який елемент V α, β в будь-якому з декількох доменів P К, має (Α β) = (α) (β) (Ка) = кА (α) Об'єктом вивчення лінійної алгебри, векторного простору у своїй власній роботі безпеки карті. Наприклад, для будь-якого лінійного простору V, гомотетічним σk: ака перетворення V лінійно, переказ не V є лінійною трансформації, якщо A1, ..., є базовим V, σ (А) = a1ja1 ... ANJ (J = 1,2, ..., N), називається σ на основі {:} матриці. Обговорення матриці лінійного перетворення може бути досягнуто за допомогою. σ на основі різних матриць схожі. Kerσ = {∈ V | σ (A) = θ} (де θ представляє нульовий вектор) називається σ ядерного, Imσ σ = {() | ∈ V} слон називається σ, σ є визначення два важливих поняття. Для евклідовому просторі, якщо σ на ортонормованій матриці ортогональні (симетричний) матриця, σ називається ортогональної (симетричний) перетворення. Ортогонального перетворення внутрішнього продукту з Павлом, Пол Лонг, конформной інші властивості, перетворення симетрії має властивість: <σ (A), β> = <a,σ(β)>. У математиці, лінійні карти (також називається лінійне перетворення або лінійним оператором) є функцією двох векторних просторів, вона залишається векторного додавання і множення. Термін "лінійне перетворення" особливо часто, особливо для векторного простору в себе від лінійного відображення (ендоморфізм). В абстрактній алгебрі, лінійне відображення гомоморфна векторний простір, або в даній області складається з векторного простору морфізм категорії. Лінійні перетворення і власних значень на розуміння Лінійне перетворення посиланням на фіг. Спочатку ми дивимося на факт. Двовимірної декартовій системі координат XOY, а потім проти годинникової стрілки кута ө стає X'OY 'пізніше, то ми дивимося на буде знайдено в XOY і X'OY "системі координат перетворення відносин між існування такого . . Тут ми надалі, щоб зрозуміти зміст цього рівняння. Ця система координат XOY в певній точці в системі координат X'OY 'координати в неї. Таким чином, ми також повинні дивитися на ці дві координати базової координат. Тобто, щоб вивчити XOY бази системи координат координатами (1,0) і (0,1) у розмірі нового системі координат X'OY 'базового прогнозу в точці з координатами (1,0) і (0,1 ), щоб вказати, як такої. (1,0) = проекції; (1,0) в проекції =;. Тоді кажуть, що перетворення координат матрицю для лінійного перетворення. Зауважимо, що матриця розташовані в передній частині двох базових перетворення координат матрицю коефіцієнтів рівняння, причина для написання транспонованою матриці відбувається тому, що ми звикли писати координувати цю базу лінійного перетворення А = (,). Ми бачимо, що мета такого перетворення повороту є турбота обертається системі координат. Такий кут повороту Після визначення, ми можемо отримати оригінальні старі координати координатних точок при новій системі координат координати. Зазначимо, що тут справа на матрицю перетворення координат. Зазначимо, що (з задньої сторони може бути додатково чітко розуміти, де обертання перетворення тільки лінійне перетворення конкретних прикладів. Більш узагальненого лінійного перетворення в наступному прикладі, ми будемо також розуміти). Тепер ми приходимо до розуміння, що таке лінійне перетворення. Його математичне визначення вищої алгебри в цілому можна знайти в книзі. (A B) = AA AB, Ака = Каа. Де А, В V в лінійному просторі (лінійний простір визначень або продовжувати бачити більш високі клуб алгебрі книги). Це визначення означає, що простір елементів (спеціально як тривимірний простір вектор) за допомогою перетворення і це перетворення лінійної характеристикою (тобто для задоволення вище, і, ставлення тривимірного обертання координатного простору була наповнена ця зв'язок, ми можемо бачити, так звана лінійна трансформація тільки дуже абстрактне одного класу конкретних перетворити колекцію з багатьох прикладів). Білінійної перетворення графів Те це перетворення переходу від одного елемента до іншого відносини відповідності елементів, ми можемо використовувати матрицю до передньої, називаються лінійними перетворення матриці. Це значення, дана зміна від одного елемента до іншого відносини перетворення елемента тільки цієї точки зору, то перед обертання координат тільки конкретний приклад лінійного перетворення тільки. Яскравий приклад лінійних перетворень занадто широким. Для того щоб проілюструвати необхідність для спини, ми повинні уважно вивчити нижче дуже цікавий приклад. У тривимірному просторі, з центром в нулі у нас є (система координат XOYZ і X'OY'Z 'з трьома кутами Ейлера не рівні нулю) сфери, сфери Звичайно, кожна точка має векторний простір , в даний час, ми нехай м'яч почав спускатися 'зміна напрямку три шпинделя, припускаючи, що X' X'OY'Z, Z 'напрям експансії, Y' бік стиснення, то ми можемо тільки уявити, що положення цих трьох напрямках вектори змінюються вздовж первісного напрямку, інший вектор положення на новому місці буде позиція вектор оригінальні під кутом. Просте і інтуїтивне розуміння цього перетворення лінійного перетворення, ми повинні розглянути наступні Проблема в тому, як описати такий процес трансформації. Безсумнівно, ми можемо використовувати матрицю перетворення для позначення будь-якого пункту на поверхні до і після зміни положення кореспонденції. Тим не менш, ми, здається, і слід було очікувати, якщо система координат X'OY'Z '(база координат), щоб описати це перетворення, то, ніж XOYZ системі координат (іншої бази координат) при перетворенні матриці простий. О, проблема в тому, що в нормальних обставинах, ми отримуємо матрицю перетворення є координати бази в матриці Загалом, як знайти цю базу зокрема погодити його, природа наша проблема. Ну, з цим основним розуміння, давайте точкою теорії річ. Вказали на попередньому двовимірної Наприклад, матриця перетворення є елементом (вектор) перетворення до іншого елемента (вектор) процесу. Отже, давайте розглянемо цей елемент є основою координат спеціальна колонка буде, які результати. Припустимо, що ми отримали таке перетворення матриці. Отже, давайте базу координат в праву (зауважимо, що це множення матриць еквівалентна правою Тензор точка вектора). Результатом є те, що базисні вектори = стати =. Лінійна формула перетворення В не-база координат з початковим напрямком вектора. Аналогічним чином, інші два буде змінено на інший напрям координат бази. Крім того, відзначимо, що якщо векторний простір (оскільки будь-який вектор може бути виражений незалежних базисних векторів, тому ми можемо природно включити розширення бази координувати загальний вектор) При цьому перетворенні отриманого перетворені координати з оригінальним відносини: =. Ми можемо уявити собі, в ролі цій матриці перетворення, можна знайти перетворення векторного простору через вчинив так, вектор, що має той же напрям, що і оригінал, але тільки її розмір має згин цього відношення, що ми часто щоб бачити. Припустимо, що такий вектор існує, то ми назвали векторів ознак, (оскільки він має лінійну характеристику перетворення напрямку і те ж), відомі характеристичні значення. Очевидно, що ми можемо використовувати перед м'ячем стає еліпсоїда уявити, що це може статися, але відзначимо, що це відбудеться або не тільки пов'язане з перетворенням самої матриці. Про матриці перетворення власних значень і векторів ми говоримо одне, конкретне метод знаходження рішення є характеристичний многочлен, власні значення отримана, вона буде повернути кожен долар зворотна рівнянь власне, щоб отримати вихідний вектор функцію. І, відзначимо, що, з такою ж фізичний зміст лінійного перетворення, для представлення різних бази перетворення координат матриця, отримана не те ж саме (обертальний перетворення Візьмемо, наприклад, припустимо, що у мене тепер є дві системи координат XOY і X'OY ', а тепер третя координата X'''' OY XOY збігається з першим, а потім повернути кут, потім ходити і трансформувати в XOY X'OY' матрицю перетворення координат чітко не збігається з системою координат для різних кути повороту не те ж саме). Тим не менш, перетворення може бути показана з іншої базової матриці перетворення координат аналогічно. І може виявитися подібних матриць мають ті ж характеристичний поліном, що означає, що ті ж характеристика перетворення полиномиального перетворення себе як зв'язок з конкретним вибір базового координат, перетворюються з характеристиками своїх. Лінійна формула перетворення Тому, природно, ми можемо по фазі запитав, якщо я міг знайти базу, що робить матриця перетворення має найбільш простий вигляд (звичайно, є діагональною матрицею). Іншими словами, чи можна знайти матрицю і діагональну матрицю схожі. Якщо так, то це те, що діагональна матриця складається. Нижче ми спочатку на припущенні, що сума на перше питання ствердно випадку, погляньте на другого завдання. Ми все ще використовуємо попередній сфері стає еліпсоїда уявити собі, що таке фізичне перетворення не збирається міняти з базовою системою координат змінилася. Тоді сфера стає еліпсоїда Наприклад, ми бачимо, що в XOY матрицю перетворення координат не просто, але якщо в якості координат бази та X'OY 'збігаються, то ця система координат, те ж саме напрямку бази координат вектор перетворюється на провідну матрицю λ разів від початкового. BY = те ж саме, ми перемикається на двох інших груп =; =. Як можна бачити, для досягнення такої зміни буде ====== 0,,,. У цьому випадку, функція вектори використовуються в якості основи в цьому випадку ми отримуємо лінійну матрицю перетворення є найбільш простим діагональну матрицю, а діагональні елементи всіх власних власних векторів, певний порядок не є строго вимоги, однак, і ви повинні вибрати той же порядок, базові координати, тобто, якщо ви оберете місце, то вона повинна також оснащені векторів, відповідних напряму X в якості базового координат. Лінійне перетворення посиланням на фіг. Ми також можемо бачити, що в тривимірному просторі, матриці перетворення для кутових три базисних вектора лінійно незалежні, то це поняття, які ми просуваємо це загальний висновок, який можна зустріти п х мірної матриці перетворення до діагональної матрицею (Або ви можете векторів ознак на основі зміни кутової координат) необхідною і достатньою умовою є те, що ви повинні мати п лінійно незалежних власних векторів. Якщо цей висновок налаштовані більш ніж матриця, то вона більш досконала, але, на жаль, не всі з матриці і його розміри складають стільки власних векторів. Тим не менш, ми можемо зробити наступні висновки. 1, що належать до різних між власними векторами є лінійно незалежними, 2, якщо характеристичне значення числа лінійно незалежних власних векторів, то ці вектори лінійно незалежні і будь-які інші різні власні характеристики лінійно не має значення. 3, діагональ матриці аналогічні умовам і розмірність матриці має стільки лінійно незалежних власних векторів. Ну, основна проблема вирішена, ми прийшли до висновку, що реальна симетрична матриця повинна бути приведена до діагонального. Нарешті ми підійшли, щоб зв'язатися з гідродинамічної точки зору, значення тензора змін в інше місце, щоб піти. Тоді тензор швидкостей деформацій і праву всередину ділянки, щоб отримати швидкості деформації. |
| Користувач Огляд |
|
Немає коментарів |